Learn How to Solve Magic Square with help of Maths !
Let's First Understand what is Magic Square
A magic square is a square grid in which distinct whole numbers are written into each cell of the grid in such a way that each horizontal row and each vertical column and each diagonal add up to the same number.
Solving 3x3 Magic Square
Watch out video here for solution
Solving with the help of Maths
It is possible to make a 3 x 3 magic square by ‘trail and test’ method, but we should try to find solution using mathematics, which will also help us to construct magic squares of higher order, e.g. 4×4 , 5×5 etc.
Read out complete solution here
Squares with just one row and one column (1 x 1) are also technically magic squares but there is nothing to play with that as that consist only one cell. Squares with two rows and columns (2 x 2) doesn’t make any magic square since it will just contradict the fact of distinct entries.
For a 2 x 2 Square to be a magic square, the sum of each row should be equal to sum of each column. If this needs to be happen in 2 x2 square, then a + b = a +c, means b = c, which contradict the fact that all the entries must be different.
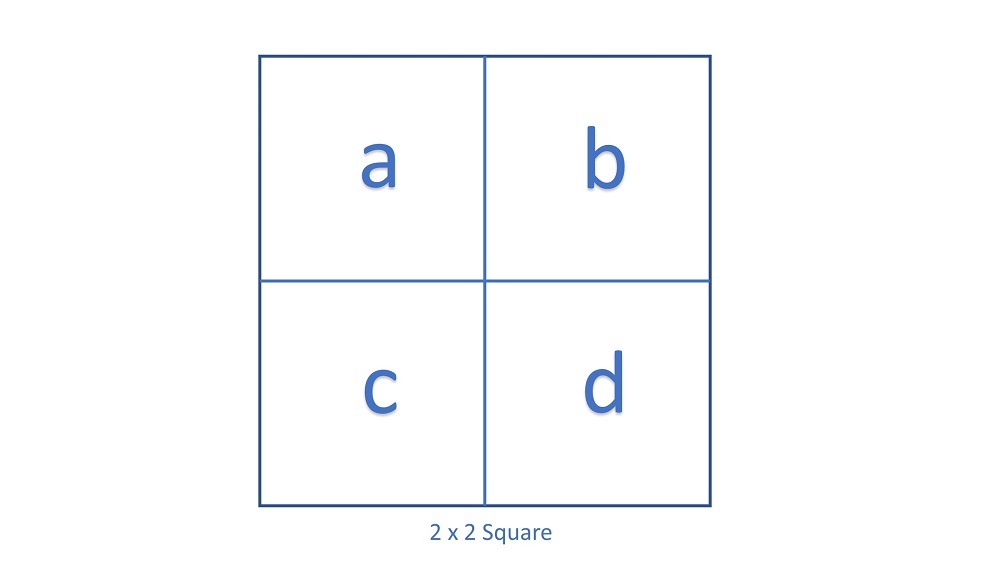
Coming next to 3 x 3 Square, we can start to form a magic square with consecutive numbers starting form 1, 2, 3, 4, 5, 6, 7, 8, 9. We have to check if we can fill each cell with these numbers such that
- Each Row, Column and Diagonal adds up to the same number
- Use Each Number Exactly Once
It is possible to make a 3 x 3 magic square by ‘trail and test’ method, but we should try to find solution using mathematics, which will also help us to construct magic squares of higher order, e.g. 4 x4 , 5 x 5 etc.
Since, we have to fill each cell with distinct number from 1 to 9, this mean that all the numbers in the grid will add to 45 ( 1+2+3+4+5+6+7+8+9 = 45) and this total would have to same as adding the totals of 3 rows or 3 columns. This shows that each row or each column or each diagonal must add up to 15. Now Let’s try to find the middle cell first, then it will become very easy to find other cell entries.
Suppose, the middle cell is ‘c’.
Now if we take middle row, middle column and two diagonals and we add these four lines, this all will together give us 15+15+15+15 = 60. Considering the other way, we can see that in total sum, all the number in the cells are included with 3 times extra ‘c’.
Therefore, we can write the equation 3c + 45 = 60, which gives us c = 5.
Now after freezing 5 in the middle, we can place other numbers in the grid considering odd and even logic. If you see that there are limited ways to get the sum as 15. It is clear that odd numbers (except 5) appear 2 times only, hence it can not appear on the corner of the square. So, we can proceed with same approach by placing other odd numbers in the middle of rows/ columns. Similarly, if you see that even numbers appear 3 times, hence it can appear on the corner of the square. So, we can proceed with same approach by placing other even numbers in the corners.
Using above method, we can have 8 possible arrangements for 3 x 3 square with distinct cell numbers from 1 to 9, which can also be obtained from one magic square by rotating numbers about the middle and / or reflecting numbers of the square in the middle row / column. This is also called ‘ Lo-Shu’ Square and was known in China around 3000 BC. It is believed that Lo Shu square was seen on the back of a small turtle surrounded by the signs of the Chinese zodiac, which emerged from the Lo river.
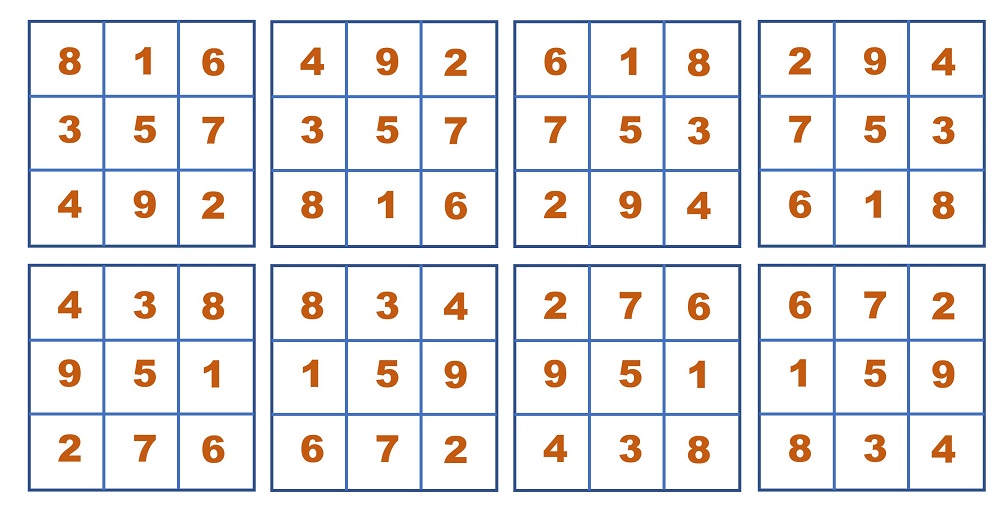
There is also one short method to fill cell entries of magic square that have odd numbers of rows and columns, which was found by French Mathematician Simon de la Loubere in the late 17th Century. This method starts by placing 1 in the middle of the first row and going up and across to place the next numbers. If it is blocked, then go back and place the number beneath the current number.
More Topics: Recommended for You
Click below and find more mathematics topics / videos :
How to Learn Maths Easily
Follow Standard Learning Approach and 10 Study Tips to Learn Maths Easily ..
Build Maths Concepts
Make your basic concepts more stronger by watching tutorials..
Free Maths Video Tutorials
Cover Course Comprehensively in a Systematic Manner with Emphasis on Basics and Concepts..
Frequently Asked Questions
Any Question with Maths ? Try to find out here. Otherwise, Ask us and we would like to help you..